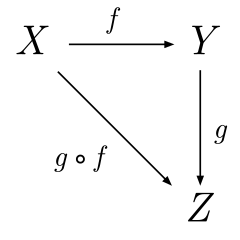presentations/monads/monads.md

title	author	aspectratio	fontsize	papersize
Monads in Haskell	Sanchayan Maity	169	14pt	presentation-16-9

Agenda

• Recap of Functors
• Recap of Applicative
• Monads

Functor

class Functor f where
    fmap :: (a -> b) -> f a -> f b
    (<$) :: a -> f b -> f a

• Must preserve identity

fmap id = id

• Must preserve composition of morphism

fmap (f . g)  ==  fmap f . fmap g

Higher order kinds

• For something to be a functor, it has to be a first order kind¹.

Applicative

class Functor f => Applicative (f :: TYPE -> TYPE) where
  pure :: a -> f a
  (<*>) :: f (a -> b) -> f a -> f b

(<$>) :: Functor f =>       (a -> b) -> f a -> f b
(<*>) :: Applicative f => f (a -> b) -> f a -> f b

fmap f x = pure f <*> x

Examples

pure (+1) <*> [1..3]
[2, 3, 4]

[(*2), (*3)] <*> [4, 5]
[8,10,12,15]

("Woo", (+1)) <*> (" Hoo!", 0)
("Woo Hoo!", 1)

(Sum 2, (+1)) <*> (Sum 0, 0)
(Sum {getSum = 2}, 1)

(Product 3, (+9)) <*> (Product 2, 8)
(Product {getProduct = 6}, 17)

(,) <$> [1, 2] <*> [3, 4]
[(1,3),(1,4),(2,3),(2,4)]

Use cases

Person
  <$> parseString "name" o
  <*> parseInt "age" o
  <*> parseTelephone "telephone" o

Can also be written as²

liftA3 Person
  (parseString "name" o)
  (parseInt "age" o)
  (parseTelephone "telephone" o)

Use cases

parsePerson :: Parser Person
parsePerson = do
  string "Name: "
  name <- takeWhile (/= 'n')
  endOfLine
  string "Age: "
  age <- decimal
  endOfLine
  pure $ Person name age

Use cases

helper :: () -> Text -> () -> () -> Int -> () -> Person
helper () name () () age () = Person name age

parsePerson :: Parser Person
parsePerson = helper
  <$> string "Name: "
  <*> takeWhile (/= 'n')
  <*> endOfLine
  <*> string "Age: "
  <*> decimal
  <*> endOfLine

Lifting

• Seeing Functor as unary lifting and Applicative as n-ary lifting

liftA0 :: Applicative f => (a)                -> (f a)
liftA1 :: Functor     f => (a -> b)           -> (f a -> f b)
liftA2 :: Applicative f => (a -> b -> c)      -> (f a -> f b -> f c)
liftA3 :: Applicative f => (a -> b -> c -> d) -> (f a -> f b -> f c -> f d)
liftA4 :: Applicative f => ..

Where liftA0 = pure and liftA1 = fmap.

Monoidal functors

• Remember Monoid?

class Monoid m where
  mempty :: m
  mappend :: m -> m -> m

($)   ::   (a -> b) ->   a ->   b
(<$>) ::   (a -> b) -> f a -> f b
(<*>) :: f (a -> b) -> f a -> f b

mappend ::     f          f      f
($) ::      (a -> b) ->   a ->   b
<*> ::    f (a -> b) -> f a -> f b

instance Monoid a => Applicative ((,) a) where
  pure x = (mempty, x)
  (u, f) <*> (v, x) = (u `mappend` v, f x)

Where are monoids again

fmap (+1) ("blah", 0)
("blah",1)

("Woo", (+1)) <*> (" Hoo!", 0)
("Woo Hoo!", 1)

(,) <$> [1, 2] <*> [3, 4]
[(1,3),(1,4),(2,3),(2,4)]

liftA2 (,) [1, 2] [3, 4]
[(1,3),(1,4),(2,3),(2,4)]

Function apply

• Applying a function to an effectful argument

(<$>) :: Functor m     =>   (a -> b)   -> m a -> m b

Applicative laws

-- Identity
pure id <*> v = v

-- Composition
pure (.) <*> u <*> v <*> w = u <*> (v <*> w)

-- Homomorphism
pure f <*> pure x = pure (f x)

-- Interchange
u <*> pure y = pure ($ y) <*> u

Operators

• pure wraps up a pure value into some kind of Applicative
• liftA2 applies a pure function to the values inside two Applicative wrapped values
• <$> operator version of fmap
• <*> apply a wrapped function to a wrapped value
• *>, <*
• See more at³

Monad, is that you?

{width=60%}

• Unreasonable Effectiveness of Metaphor⁴

Motivation - I

safeInverse :: Float -> Maybe Float
safeInverse 0 = Nothing
safeInverse x = Just (1 / x)

safeSqrt :: Float -> Maybe Float
safeSqrt x = case x <= 0 of
  True -> Nothing
  False -> Just (sqrt x)

sqrtInverse1 :: Float -> Maybe (Maybe Float)
sqrtInverse1 x = safeInverse <$> (safeSqrt x)

Motivation - I

joinMaybe :: Maybe (Maybe a) -> Maybe a
joinMaybe (Just x) = x
joinMaybe Nothing = Nothing

sqrtInverse2 :: Float -> Maybe Float
sqrtInverse2 x = joinMaybe $ safeInverse <$> (safeSqrt x)

-- In general
-- join :: Monad m => m (m a) -> m a

Motivation - II

(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
x >>= f = case x of
  (Just x') -> f x'
  Nothing -> Nothing

sqrtInverse :: Float -> Maybe Float
sqrtInverse x = (>>=) (safeSqrt x) safeInverse

-- >>= is also known as `bind`

-- In general
-- (>>=) :: Monad m => m a -> (a -> m b) -> m b

Motivation - III

(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
  Just x -> g x
  Nothing -> Nothing

sqrtInverse3 :: Float -> Maybe Float
sqrtInverse3 = safeSqrt >=> safeInverse

-- In general
-- (>=>) :: Monad m => (a -> m b) -> (b -> m c) -> (a -> m c)

Motivations

• Flattening
• Sequencing
• Composition

Monad

class Applicative m => Monad (m :: Type -> Type) where
  return :: a -> m a
  (>>=) :: m a -> (a -> m b) -> m b

import Control.Monad (join)

join :: Monad m => m (m a) -> m a

Just do

main :: IO ()
main = do
  putStrLn "What is your name?"
  name <- getLine
  let greeting = "Hello, " ++ name
  putStrLn greeting

Monad laws

-- Left identity
return x >>= f == f x

-- Right identity
x >>= return == x

-- Associativity
m >>= (\x -> k x >>= h) == (m >>= k) >>= h

???

{width=60%}

Monoids recap

class Semigroup m where
  (<>) :: m -> m -> m

class Semigroup m => Monoid m where
  mempty :: m

  -- defining mappend is unnecessary, it copies from Semigroup
  mappend :: m -> m -> m
  mappend = (<>)

Some Math

{width=30%}

• Category: a set of objects and arrows
• Arrows between objects (morphisms): functions mapping one object to another
• Two categories: Set and Hask

Categories

• Set
  • Category of sets
  • Every arrow, function from one set to another
• Hask
  • Similar to Set
  • Objects are Haskell types like Int instead of Z or R
  • Arrows between objects a & b are functions of type a -> b
  • a -> b also a Type in Hask
  • If A -> B and B -> C, then A -> C ~= . in Hask
  • Fun fact: Function composition forms a monoid! (See Endo).

Monads are monoids...

In Haskell

• Only work with Hask, so functors all map back to Hask.

• Functor typeclass are a special type of functor called endofunctors

• endofunctors map a category back to itself

• Monad is a monoid where

-- Operation
>==>

-- Identity
return

-- Set
Type
a -> m b

Now?

{width=80%}

Contrasts with Monad

• No data dependency between f a and f b
• Result of f a can't possibly influence the behaviour of f b
• That needs something like a -> f b

Applicative vs Monads

• Applicative

  • Effects
  • Batching and aggregation
  • Concurrency/Independent
    • Parsing context free grammar
    • Exploring all branches of computation (see Alternative)

• Monads

  • Effects
  • Composition
  • Sequence/Dependent
    • Parsing context sensitive grammar
    • Branching on previous results

Weaker but better

• Weaker than monads but thus also more common
• Lends itself to optimisation (See Facebook's Haxl project)
• Always opt for the least powerful mechanism to get things done
• No dependency issues or branching? just use applicative

State monad

newtype State s a = State { runState :: s -> (a, s) }

instance Functor (State s) where
  fmap :: (a -> b) -> State s a -> State s b
  fmap f (State sa) = State $ \s -> let (a, s) = sa s in (f a, s)

instance Applicative (State s) where
  pure :: a -> State s a
  pure a = State $ \s -> (a, s)

  (<*>) :: State s (a -> b) -> State s a -> State s b
  State f <*> State g = State $ \s -> let (aTob, s') = f s in
                                          let (a, s'') = g s' in
                                              (aTob a, s'')

State monad

instance Monad (State s) where
  return = pure
  (>>=) :: State s a
        -> (a -> State s b)
        -> State s b
  (State f) >>= g = State $ \s -> let (a, s') = f s
                                      ms = runState $ g a
                                  in ms s'
  (>>) :: State s a
       -> State s b
       -> State s b
  State f >> State g = State $ \s -> let (_, s') = f s
                                     in g s'

get :: State s s
get = State $ \s -> (s, s)

State monad

put :: s -> State s ()
put s = State $ \_ -> ((), s)

modify :: (s -> s) -> State s ()
modify f = get >>= \x -> put (f x)

eval :: State s a -> s -> a
eval (State sa) x = let (a, _) = sa x
                    in a

Context

type Stack = [Int]

empty :: Stack
empty = []

pop :: State Stack Int
pop = State $ \(x:xs) -> (x, xs)

push :: Int -> State Stack ()
push a = State $ \xs -> ((), a:xs)

tos :: State Stack Int
tos = State $ \(x:xs) -> (x, x:xs)

Context

stackManip :: State Stack Int
stackManip = do
    push 10
    push 20
    a <- pop
    b <- pop
    push (a+b)
    tos

testState = eval stackManip empty

Reader monad

class Monad m => MonadReader r m | m -> r where
  ask :: m r
  local :: (r -> r) -> m a -> m a

Context

import Control.Monad.Reader

tom :: Reader String String
tom = do
    env <- ask
    return (env ++ " This is Tom.")

jerry :: Reader String String
jerry = do
  env <- ask
  return (env ++ " This is Jerry.")

Context

tomAndJerry :: Reader String String
tomAndJerry = do
    t <- tom
    j <- jerry
    return (t ++ " " ++ j)

runJerryRun :: String
runJerryRun = runReader tomAndJerry "Who is this?"

Questions

• Reach out on
  • Email: me@sanchayanmaity.net
  • Mastodon: sanchayanmaity.com

---

1. Haskell's Kind System ↩︎

2. FP Complete - Crash course to Applicative syntax ↩︎

3. FP Complete - Crash course to Applicative syntax ↩︎

4. The Unreasonable Effectiveness of Metaphor ↩︎